1° Forum di Astronomia Amatoriale Italiano

AndMan, però, se metti a fianco a quelle due anche la foto di Angelo che compare in questo stesso thread la differenza c'è e non è poca download/file.php?id=30034&mode=view
Le strutture sulla zona equatoriale sono molto più ricche di particolari in quella di Angelo e i bordi delle bande sono più nette.Nella NEB si risolvono delle minute striature a basso contrasto inclinate a 45° che non ci sono né nella tua né in quella di Go.
Hai ottenuto degli ottimi risultati per un 10", ma io continuo a vedere un certo vantaggio a favore del 14".

Spremere un 10" fino al limite è più facile che spremere un 14" fino al limite. Come ho detto la probabilità di ottenere una immagine diffractoin limited dipende dal rapporto D/r0. E' spiegato qua http://www.astrosurf.com/cavadore/optiq ... index.html (per Pietro: questo è lo stato dell'arte che sta alla base delle ottiche adattative).


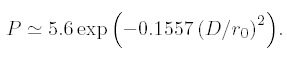
Facciamo il confronto in base a questa "teoria": Mettiamo un 10" e un 14". Vediamo quante immagini diffraction limited si possono ottenere con diversi gradi di seeing.
Prima di fare il confronto va fatta una precisazione che riguarda il concetto di "diffraction limited" seconbdo Fried. La formula siopra, elaborata da Fried, fornisce la probabilità che un frame di durata infinitesima soddisfi la condizione che l'errore rms sia minore di 1/6.28.
Cioè:
a) i frames devono essere esposti per un tempo molto breve, che deve essere minore del tempo di coerenza della turbolenza (tipicamente centesimi se non millesimi di secondo). Questa condizione non viene soddisfatta quasi mai. In una tipica esposizione di 1/15 di secondo l turbolenza si muove (non viene congelata) e la probabilità di ottenere un frame diffraction limited è quindi minore di quanto fornito dalla teoria. In ogni caso se si espone con tempi più brevi (per esempio 1/60) ci si avvicina alla condizione ideale.
b) il criterio di qualità per Fried è 1/6.28 rms che è bassino (rispetto a 1/14 che è il criterio di Rayleigh). Fried calcola la probabilità di ottenere delle immagini "discrete". Ovviamente avrebbe potuto calcolare la probabilità di ottenere immagini a 1/14 rms ma sarebbe stata più bassa.
Il numeretto che esce dalla formula è quindi una stima della frazione di immagini "buone" secondo il criterio sopra precisato. Una parte di queste saranno ottime nel senso che raggiungono il criterio 1/14. Ci saranno poi altre immagini di qualità via via decrescente.

Chiarito questo facciamo il confronto delle due aperture.

Facciamo prima il caso di seeing cattivo. Diciamo che r0 sia 5 cm. Usando la formula sopra otteniamo la frazione di frame "buoni" prodotti da una apertura di 25 cm e da una apertura di 36 cm. Ci metto anche una apertura di 30 cm che mi serve dopo per il ragionamento.

25 cm -> 11.4%
30 cm ->2%
36 cm -> 0.17%

Come si vede, con seeing "cattivo" su 1000 frames ce ne saranno 114 che raggiungono la qualità di una apertura di 25 cm, 20 che raggiungono la qualità di una apertura di 30 cm e nessuno che raggiunge la qualità consentita da una apertura di 36 cm.
Con un telescopio di 25 cm si possono avere frames che si avvicinano al limite di questo telescopio. Al contrario con un telescopio di 36 cm non si ottengono mai frames che si avvicinano al suo limite. Il 36 cm raccoglierà gli stessi 114 frames buoni del 25 cm e una parte di questi, precisamente 20 saranno anche migliori raggiungendo la qualità di 30 cm ma nessun frame sarà tale da sfruttare appieno la potenza del 36 cm.
Non è quindi esatto dire che il 36 cm rende come il 25, perchè un sesto dei frames (20 su 114) è comunque superiore a quelli ottenibili da 25. E' esatto invece dire che il seeing pessimo ha sostanzialmente appiattito le prestazioni.
A questo punto andebbe però riconsoderato il fatto che il 36 cm opera con tempi di esposizione più brevi e quindi i famosi 114 frame sono più "mossi" nel 25 cm. Se per esempio il tempo di coerenza fosse 1/90 secondo e il 25 operasse a 1/15 avrebbe una esposizione che dura 6 volte il tempo di coerenza. Come prendere 6 frames di 1/90 di fila e sommarli assieme senza riallineali. Non tutti questi saranno buoni. Se il 36 cm opera invece a 1/30s ha una esposizione che dura solo tre volte il tempo di coerenza ed sarebbe come prendere tre frames da 1/90sdi fila e sommarli senza allinearli (certamente meglio no). Quindi, per questo solo fattore tutti i frames "buoni" del 25" sono meno "buoni" che nel 36 cm e sono a loro olta meno buoni della condizione ideale in cui la turbolenza è congelata perfettamente.

Facciamo adesso il caso di un seeing decente. r0=10 cm. Oteniamo queste probabilità.

25 cm -> ~100%
30 cm ->~100%
36 cm -> 74.4%

Con un seeing di 1.2" praticamente tutti i frames raggiungono la qualità di una apertura di 30 cm e il 74.4% raggiunge la qualità di 36 (sempre nel senso lambda/6.26 rms). Fra questi ce ne saranno molti che raggiungo anche qualità superiori come lambda/14 rm (cioè diffraction limited secondo Rayleigh).
In questo caso non c'è storia perché il 36 cm può essere sfruttato al 100% delle sue possibilità.
Se il seeing migliorasse ulteriormente, il 36 potrebbe ancora migliorare, il 25 no, perchè è già al 100% delle sue possibilità.
Ipotetici seeing miracolosi possono avvantaggiare solo le grandi aperture.

Si va bene .

_________________
Dall-Kirkham 14" f/20 su AlterD6 "coming soon"Flea3 ICX618 mono - Baader LRGB filters - RG610nm- IrPass 685/807nm

Finalmente si e arreso.


" Questa rende meglio "

_________________
IOptron iEQ45 PRO
MEADE ACF da 30cm.
Asi120-s +Asi 224 Mc.

Si riparte!!!!!

http://www.astrobin.com/users/AngeloGentile/

Angelo,

basta a postare queste immagini altrimenti qualcuno rischia di fallire per mancata vendita!

E poi si sà che questi C14 sono pieni di difetti...abbiamo avuto tutti poco cervello nell'averlo acquistato...e soprattutto ci facciamo troppe pippe mentali con meccaniche e ottiche superlative mentre gli altri con certi telescopi fanno immagini stellari (non le vedi pubblicate in tutti i forum del mondo?!?)

Come diceva qualcuno ci vogliono fatti e non pugnette!

_________________
Alessandro Bianconi
http://www.astrobin.com/users/sulcis2000/

Ottengo sempre quel che voglio

Osservo con:
C14 EDGE
Starizona Hypestar
10 Micron GM2000QCI
Astro Professional 152/900 with internal D-ERF 75
Daystar Quark Chromosphere Version
TS60ED
Skywatcher NEQ6
Starlight Trius H694 mono
ASI224MC
ASI174MM

Intanto posto questo capolavoro di Diametro, POtenza, Seeing, e Tele prettamente commerciale.
E inutile che cito l'autore tanto si intuisce da solo.


http://www.foto-astronomia.it/applicazi ... 0817j1.jpg


" Ma guarda un altro C14 "

_________________
IOptron iEQ45 PRO
MEADE ACF da 30cm.
Asi120-s +Asi 224 Mc.

Si riparte!!!!!

http://www.astrobin.com/users/AngeloGentile/

Andrea, la variazione che osservi in una lista di foto come l'ALPO è dovuta a tanti fattori. Li elenco secondo me nell'ordine di importanza:

- condizioni di seeing locale e condizioni termiche.
- esperienza dell'osservatore nel gestire il telescopio.
- apertura del telescopio
- qualità del telescopio
- sistema di ripresa
- esperienza dell'operatore nel gestire la ripresa e il processing

e forse ho dimenticato qualche cosa.

Quando si osservano delle fluttuazioni nella resa di un certo telescopio non per questo si può concludere che la causa sia uno di quei fattori da solo. Lo stesso telescopio renderebbe in maniera diversa in mano a persone diverse in luoghi diversi e momenti diversi e non perché la resa del telescopio varia da momento a momento, ma proprio per l'esperienza dell'osservatore, ecc ecc.
Ti faccio solo un esempio nel campo visuale, dove la leggenda che i riflettori non fossero adatti per l'alta risoluzione qualche anno fa sembrava cosa assodata (al punto che si raccomandavano perfettissimi rifrattori di apertura risibile). Con il tempo si è capito che la maggioranza degli astrofili non sapeva ancora nulla delle problematiche termiche e scambiava tutto per "seeing". L'esperienza conta.
Se vuoi avere un'idea delle potenzialità di un certo telescopio devi prendere le migliori immagini che sono state prodotte con quel telescopio, perchè solo quando tutti i fattori che si possono controllare sono stati opportunamente controllati quello che resta è il limite del telescopio.
La differenza fra Marco Guidi e un mediocre C14 si chiama "Marco Guidi". Il tubo è lo stesso.

Mauro@
Se, come affermi, il diametro dovrebbe farla da padrone con qualsiasi seeing, concetto che non fatico ad accettare, come spieghi questa inversione dichiarata da Ale?
<<Ragazzi
vorrei proporvi una mia graduatoria in termini di risoluzione/percezione dettagli/contrasto/luminosità di alcune delle ottiche più rappresentative per l'hires da me possedute paragonandole l'una con l'altra in base alle varie condizioni di seeing (parlo di paragoni validi per l'imaging hires ma penso che lo stesso paragone possa esser tranquillamente esteso anche per il visuale)

In caso di SEEING inferiore ai 4/10

1) TEC160ED
2) Intes Micro MN 78
3) Tripletto Tecnosky 115/800
4) Intes Micro Deluxe Mak 258/3870
5) Dall Kirkham Ariete 315/5040
6) Celestron C14HD edge

In condizioni di seeing medie (tra 5-6/10)

1) TEC160ED
2) Intes Micro Deluxe Mak 258/3870
3)/4) Dall Kirkham Ariete 315/5040 - Intes Micro MN 78
5) Celestron C14HD edge
6) Tripletto Tecnosky 115/800 >>


Ciao,
P

A mano a mano che le differenze si assottigliano, fattori come l'acclimatamento imperfetto potrebbero interferire. Può essere che Ale abbia avuto questa impressione anche in più e più volte.
Io ho fatto molte prove con diaframmi in diverse condizioni. Ti posso per esempio dire che la quantità di luce raccolta influenza il giudizio, nel senso che quando si mette un diaframma maggiore si vede meglio tutto, compri piccoli sbuffi di luce che altrimenti non si sarebbero visti (ci sono lo stesso se poi si guarda con attenzione e sono proporzionati alla luce raccolta). E' un po' come aumentare il volume nella riproduzione di un brano con rumore. Non è che l'aumento di volume peggiora la qualità del brano (il segnale e il rumore son nello stesso rapporto) ma poichè si sente il rumore si può in un primo momento pensare che sia peggio.

Poi la questione delle prestazioni con seeing pessimo è una questione di tipo "accademico" giacchè con seeing pessimo non si ottine granché in nessun caso. Non c'è comunque un telescopio o schema ottico che possa risentire meno del seeing di un altro. La dipendenza dal seeing è cosa ben conosciuta nella letteratura scientifica e dipende dal rapporto D/r0 e basta (non dal colore del tubo, dal tipo di vetri o dallo schema ottico). In imaging un secondo paramtetro è il rapporto fra il tempo di esposizione e il tempo di correlazione della turbolenza che è r0/V dove V è la velocità di trascinamento dello strato turbolento (si chiama Taylor screen perchè è come se ci fosse una finestra irregolare che scorre davanti al telescopio). Fatti conto che con r0=10 cm e V=10 m/s questo tempo è 0.01 s ed è il tempo necessario pr congelare la turbolenza. Nessuno espone a questi tempi per cui la turbolenza ha sempre un certo mosso. Ma un conto è esporre a 0.02 s altro a 0.1.

Pietro

la classifica da me esposta è frutto della MIA esperienza personale e in quanto tale è relativa e non assoluta (detto in soldoni non è lex!)
Ciò che può esser considerato assoluto è il frutto delle immagini realizzate con i propri telescopi.
Se tu fai un giro fra i vari forum, italiani, americani, australiani ti farai una tua idea di quali ottiche performano bene e quali no. Io a mio parere vedo tanti C14 e di conseguenza se la statistica non è una barzelletta penso che poi tutto sommato non sono tanto malaccio per realizzare OTTIME immagini in alta risoluzione (e non mi si dica che non si vedono DK da 14" artigianali perchè questi costano tanto ma se ci fossero performerebbero meglio...queste sono solo affermazioni legate al marketing di chi li progetta...perchè non si mettono loro a realizzare signore immagini così vediamo se EFFETTIVAMENTE performano meglio...)

Ma in fin dei conti con tutta questa miriade di post che abbiamo aperto di che cosa stiamo parlando? Io son del parere che se il nostro obiettivo è realizzare belle immagini allora mettiamoci sotto e realizziamole anzichè argomentare su meccaniche, mirror flop, raggiungimento equilibrio termico, fibre in carbonio, celle a 18 punti di appoggio...facciamo immagini e poi valutiamo SUI RISULTATI REALI ovvero sulle IMMAGINI realizzate e non sull'acqua fritta

Ripeto...se mi è concesso con un francesismo..."fatti e non pugnette"

_________________
Alessandro Bianconi
http://www.astrobin.com/users/sulcis2000/

Ottengo sempre quel che voglio

Osservo con:
C14 EDGE
Starizona Hypestar
10 Micron GM2000QCI
Astro Professional 152/900 with internal D-ERF 75
Daystar Quark Chromosphere Version
TS60ED
Skywatcher NEQ6
Starlight Trius H694 mono
ASI224MC
ASI174MM

Grazie ad Ale e a Mauro per le risposte...
Ciao,
Pietro